積立投資で活用したい１２６の法則！着実に効率よく資産形成を始めよう！

こんにちは、ファイナンシャル・プランナーの hiro です。

投資における72の法則と126の法則をご存じでしょうか。

長期投資のメリットとして、長期的に運用を行うことで複利の効果を得られることにあります。資産運用における複利効果で元本が2倍になるまでの期間が簡単に計算できる法則に72の法則があります。

72の法則を付け加えて解説すれば、今ある資産を一括投資したときに元本が 2倍になる期間が計算できる法則です。そのため、積立投資には適用されません。

そこで今回は、積立投資による積み立てた元本が 2倍になる期間が簡単に計算できる 126の法則について解説します。

着実に効率よく資産形成を始めましょう。

積立投資における126の法則とは

利息の計算方法には単利と複利の2種類があります。

単利とは、当初の元本に対してのみ利息を計算する方式です。それに対し複利では、一定期間ごとに支払われる利息を元本に含めて、これを新しい元本として利息を計算する方式になります。利息が利息を生むいわゆる複利効果によって、利率や期間など同じ条件の単利の商品よりも受取時の元利合計額は多くなります。

そして、その複利効果によって元本が2倍になる期間が簡単に計算できる法則が72の法則と126の法則になります。

72の法則（一括投資）

一括投資した場合に、複利効果で元本が 2倍になるまでの期間が簡単に計算できる法則に72の法則があります。

【72の法則（一括投資）】
72÷利率＝元本が2倍になるまでに要する年数

この72の法則を活用することで「一括投資した元本が2倍になるまでの期間」を計算できるだけでなく「運用期間から一括投資した元本が2倍になるための利率」も計算することができます。

利率から期間を計算	期間から利率を計算
利率2％：72÷2＝36年	期間10年：72÷10＝7.2％
利率3％：72÷3＝24年	期間20年：72÷20＝3.6％
利率4％：72÷4＝18年	期間30年：72÷30＝2.4％
利率5％：72÷5＝14.4年	期間40年：72÷40＝1.8％

このように 72の法則を活用することで、一括投資した元本が2倍になるために必要な期間や利率を簡単に計算することができるのです。

126の法則（積立投資）

72の法則は便利ですが、あくまで一括投資を行う前提のもとで元本が2倍になるまでの期間を計算するもので、積立投資には当てはまりません。そこで、積み立てた元本が2倍になるまでの年数や利率が簡単に計算できる126の法則について慶應義塾大学理工学部の枇々木規雄教授がレポートを発表されたのです。

【126の法則（積立投資）】
126÷利率＝積立元本が2倍になるまでに要する年数

この126の法則を活用することで「積立投資した元本が 2倍になるまでの期間」を計算できるだけでなく「運用期間から積立投資した元本が 2倍になるための利率」も72の法則と同じように計算することができます。

利率から期間を計算	期間から利率を計算
利率2％：126÷2＝63年	期間10年：126÷10＝12.6％
利率3％：126÷3＝42年	期間20年：126÷10＝6.3％
利率4％：126÷4＝31.5年	期間30年：126÷10＝4.2％
利率5％：126÷5＝25.2年	期間40年：126÷10＝3.15％

このように126の法則を活用することで、積立投資した元本が 2倍になるために必要な期間や利率を簡単に計算することができるのです。

126の法則（積立投資）を活用した積立イメージ

126の法則を活用することで、積立投資した元本が2倍になるために必要な期間や利率を簡単に計算することができます。実際に126の法則を活用した積立をイメージしてみましょう。

積立期間	利回り	積立金額（月）	積立元本	目標金額
23歳から65歳まで（42年間）	3.00％	20,000円	10,800,000円	20,160,000円

「23歳から65歳まで42年働くとして、働き始めてすぐに積立投資を始め、平均的に利率3％で投資できれば、おおよそではあるが、積立額は半分で済むと考えるとわかりやすいだろう」と、枇々木教授は解説しています。

運用期間が短い場合やリスク許容度が低い場合には「76の法則」「43の法則」も

前節で解説した126の法則では、積立元本が2倍になるまで42年間3％程度の運用が必要でしたが、40代・50代の方がこれから積立投資を始めて積立元本の2倍を目指すとすると、例えば積立期間が20年間では6.3％での運用が必要になります。

佐々木教授は、126の法則以外にも他の法則も紹介されています。運用期間が短い場合やリスク許容度が低い場合には、積立元本が 1.5倍となる76の法則や、積立元本が1.25倍となる43の法則などもあります。

積立元本が1.5倍となる76の法則

利率から期間を計算	期間から利率を計算
利率2％：76÷2＝38年	期間10年：76÷10＝7.6％
利率3％：76÷3＝25.3年	期間20年：76÷20＝3.8％
利率4％：76÷4＝19年	期間30年：76÷30＝2.53％
利率5％：76÷5＝15.2年	期間40年：76÷30＝1.9％

積立元本が1.25倍となる43の法則

利率から期間を計算	期間から利率を計算
利率2％：43÷2＝21.5年	期間10年：43÷10＝4.3％
利率3％：43÷3＝14.33年	期間20年：43÷20＝2.15％
利率4％：43÷4＝10.75年	期間30年：43÷30＝1.43％
利率5％：43÷5＝8.6年	期間40年：43÷40＝1.07％

126の法則・72の法則の注意点

ここまで126の法則・72の法則について解説してきましたが、投資においてはリスクがあります。投資におけるリスクとは、一般的な「危険なこと」「避けるべきこと」という意味ではなく「リターンが不確実である（予測できない）こと」を表します。

いくら積立投資した元本が2倍になる計画を立てたとしても、リスクが大きい（振れ幅が大きい）場合には計画どおりに元本が増えないこともあります。つまりこの126の法則・72の法則ではリスクは考慮されていないことに注意が必要です。

126の法則・72の法則ともリスクは考慮されていないことに注意

枇々木教授は、値動きが小さいほうが法則に近い効果が得られやすいので、その意味においては分散投資によって値動きを抑えるのが望ましいとの解説をされています。

広告リンク

リスクとリターンの関係

前章でも解説したとおり、投資におけるリスクとは「リターンが不確実である（予測できない）こと」を表します。一方、投資におけるリターンとは「資産運用を行うことで得られる収益」のことです。

不確実の度合い（振れ幅）が大きいことを「リスクが大きい」といい、「大きく収益が得られるかもしれないし、大きく損失が出るかもしれない」ということを表しています。

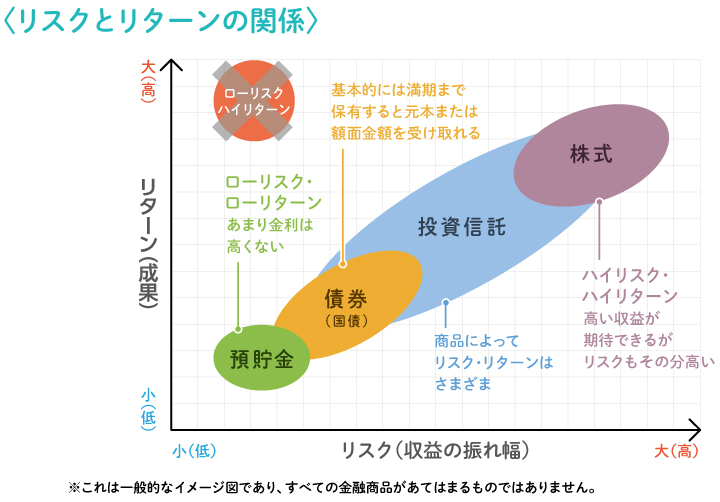
リスクとリターンの関係は比例関係にあり、リスクを低く抑えようとするとリターンは低下し、高いリターンを得ようとするとリスクも高まります。

しかし、分散投資を行うことによって、リスクを分散させ、ひとつの市場でのリスクが全体の投資に与える影響を緩和することができます。つまり、分散投資を行うことで、リスクの低減だけでなく、より安定したリターンを得ることにつながります。そうした意味でもリスクを抑えるための分散投資が重要といえます。

広告リンク

まとめ｜積立投資で活用したい １２６の法則

今回は、今ある資産を一括投資したときに元本が 2倍になる期間が計算できる72の法則、そして積立投資による積み立てた元本が 2倍になる期間が簡単に計算でき126の法則について解説してきました。

72の法則 （一括投資）	126の法則 （積立投資）
72÷利率＝元本が2倍になるまでに要する年数	126÷利率＝積立元本が2倍になるまでに要する年数

積立投資した元本が2倍になる計画を立てたとしても、リスクが大きい（振れ幅が大きい）場合には計画どおりに元本が増えないこともあります。つまりこの126の法則・72の法則ではリスクは考慮されていないことに注意が必要です。しかしながら、分散投資を行うことで、リスクの低減だけでなく、より安定したリターンを得ることにつながります。そうした意味でもリスクを抑えるための分散投資が重要といえます。

分散投資を行い、リスクを低減させ適切なリターンを得ることで、着実に効率よく資産形成を進めていきましょう。

最後までお読みいただきありがとうございました。